Mapa conceptual

Descargar

Infografía de las aplicaciones que ofrece Google y microsoft

"GRAFICAR FUNCIONES LINEALES Super facil"

Para que te sea más fácil entenderlo te dejaré un video en el que te explica paso a paso como graficar una función lineal.

ESPERO TE SEA DE UTILIDAD!!!

SEGUIMOS CON MAS FUNCIONES!!!!

Puntos de corte con los ejes

Una función lineal siempre corta al eje Y en un punto. También, corta al eje X en un punto.

El punto de corte con el eje Y es el punto de la recta que tiene la primera coordenada igual a $0$:

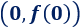
El punto de corte con el eje X es el punto de la recta que tiene $0$ en la segunda coordenada. Se calcula igualando a $0$ la función y resolviendo la ecuación obtenida.

Ejemplo

Calculamos los puntos de corte de la función del ejemplo anterior,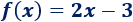

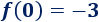
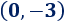
Corte con el eje Y:

Es el punto

Observad que la segunda coordenada es la ordenada.
Corte con el eje X:

Es el punto

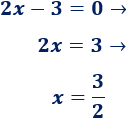
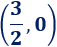
 Función a partir de dos puntos

Si tenemos dos puntos de la recta, podemos calcular la expresión algebraica de la función. Sólo tenemos que sustituir las coordenadas de los puntos en la forma general de la función

y resolver el sistema de ecuaciones.

Ejemplo

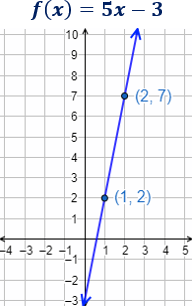
Vamos a calcular la función lineal que pasa por los puntos $(1,2)$ y $(2,7)$.
Tenemos que hallar la pendiente, $m$, y la ordenada, $n$.
Primer punto
Como $x=1$ e $y=2$, sustituyendo,

Segundo punto
Como $x=2$ e $y=7$, sustituyendo,

Tenemos el sistema

Resolviendo el sistema, por ejemplo, por reducción, tenemos que $m=5$ (con lo que $n=-3$). Por tanto, se trata de la función

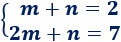
 Intersección de dos funciones

Si tenemos dos funciones lineales, podemos preguntarnos si las rectas que representan se cortan y en qué punto lo hacen.

Para responder esta pregunta, sólo tenemos que igualar las dos expresiones algebraicas y resolver la ecuación.

Ejemplo

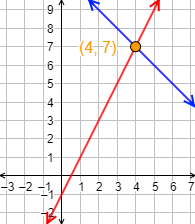
Vamos a calcular el punto de corte de las dos siguientes rectas: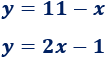

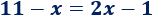
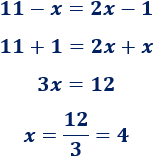
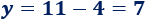
Como $y=y$, igualando,

Resolvemos la ecuación:

La primera coordenada del punto de corte es $x=4$. La segunda coordenada la obtenemos calculando su imagen en alguna de las dos rectas:

Por tanto, el punto de corte es $(4,7)$.
Gráfica:

 Paralelas y perpendiculares

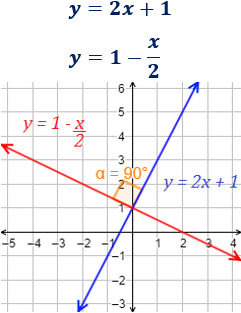
Dos rectas son paralelas si no se cortan en ningún punto (o si son iguales). Esto ocurre cuando tienen la misma pendiente, $m$.

Dos rectas son perpendiculares si se cortan formando un ángulo recto (ángulo de 45°). Las rectas perpendiculares a la recta con pendiente $m$ son las que tienen pendiente $-1/m$.

Ejemplo

Las siguientes rectas son paralelas porque tienen la misma pendiente ($m=2$):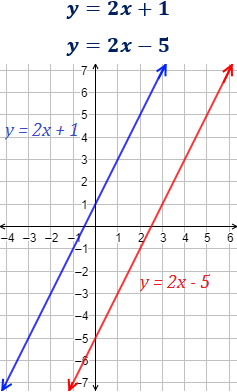

Las siguientes rectas son perpendiculares porque la pendiente de la una es el opuesto del inverso de la pendiente de la otra:

MÉTODO 2 FUNCIONES LINEALES

Método 2
Método 2: Grafica funciones lineales en su forma no estándar

1. 
   1
   Arregla la función para hacer que la Y sea el sujeto. Si tienes una función lineal que no está en su forma estándar, deberás reescribirla antes de poder hacer el gráfico.

   • Digamos que tienes la función 6x – 2y = 4. Mueve todo menos la Y a la izquierda de la siguiente manera.
     
   • Luego divide ambos lados entre -2. Ahora tienes la forma estándar de una función lineal: y = 3x – 2.
     
2. 
   2
   Busca por lo menos dos puntos. Sabrás que tu gráfico tendrá una línea recta porque tienes una función lineal, por lo tanto, realmente solo necesitas dos puntos. En general, sin embargo, debes encontrar 3 puntos en lugar de 2 para revisar la precisión.

   • En el ejemplo reescrito más arriba, quizá puedas elegir -1, 0 y 1 como valores de X. Resuelve de la siguiente manera.
     
3. 
   3
   Dibuja los puntos. Coloca los puntos en el sistema de coordenadas utilizando los valores que obtuviste al resolver las 3 ecuaciones.

   • En el ejemplo anterior, los puntos deben verse así.
     
4. 
   4
   Conecta los puntos. Para 2 puntos cualesquiera, solo hay una forma de conectarlos con una línea recta. Utiliza una regla para unirlos con una línea. Debes notar que si graficas 3 puntos y no todos caen en la misma línea, has cometido algún error. Regresa y calcula todo de nuevo.

   • En el ejemplo anterior, el gráfico debe verse así.
     
   
   

Consejos

• Las funciones tienen una variable independiente “X” y una variable dependiente “Y”. La pendiente de una recta que pasa a través de los puntos (x1, y1) y (x2, y2) se calcula de la siguiente forma.
  
• Las funciones lineales tienen muchas aplicaciones prácticas, especialmente en la economía.